This post is primarily intended for the students in Julie's EPMA class, but there is an interesting twist at the end so even experts might be amused to read through.
The new EDS flags in PFE that are automatically enabled in Probe for EPMA when Bruker or Thermo EDS acquisitions are performed seem to be working great for the students. Using EDS quant with WDS quant in PFE is quite easy now.
In fact we even discovered another helpful bit of code when the students were setting up a quant lab practical yesterday doing trace elements on WDS and major elements by EDS when we added our trace elements by WDS first, and then we added an element by EDS before we had even acquired an EDS spectrum. The software then popped up a little message saying that we had forgotten to turn on the "acquire EDS spectra" checkbox, and telling us that it turned it on for us automatically!
Such a nice software!

So here are the results of our integrated EDS-WDS lab practical measuring Rb and Ti in a synthetic quartz. The idea being to measure Rb and Ti as trace elements using EDS and Si using WDS just to obtain a decent matrix correction. Specifically: how accurately can we measure "zero" Rb when there is a significant interference of Si Ka on Rb La? First lets look at the wavescan on Rb La:

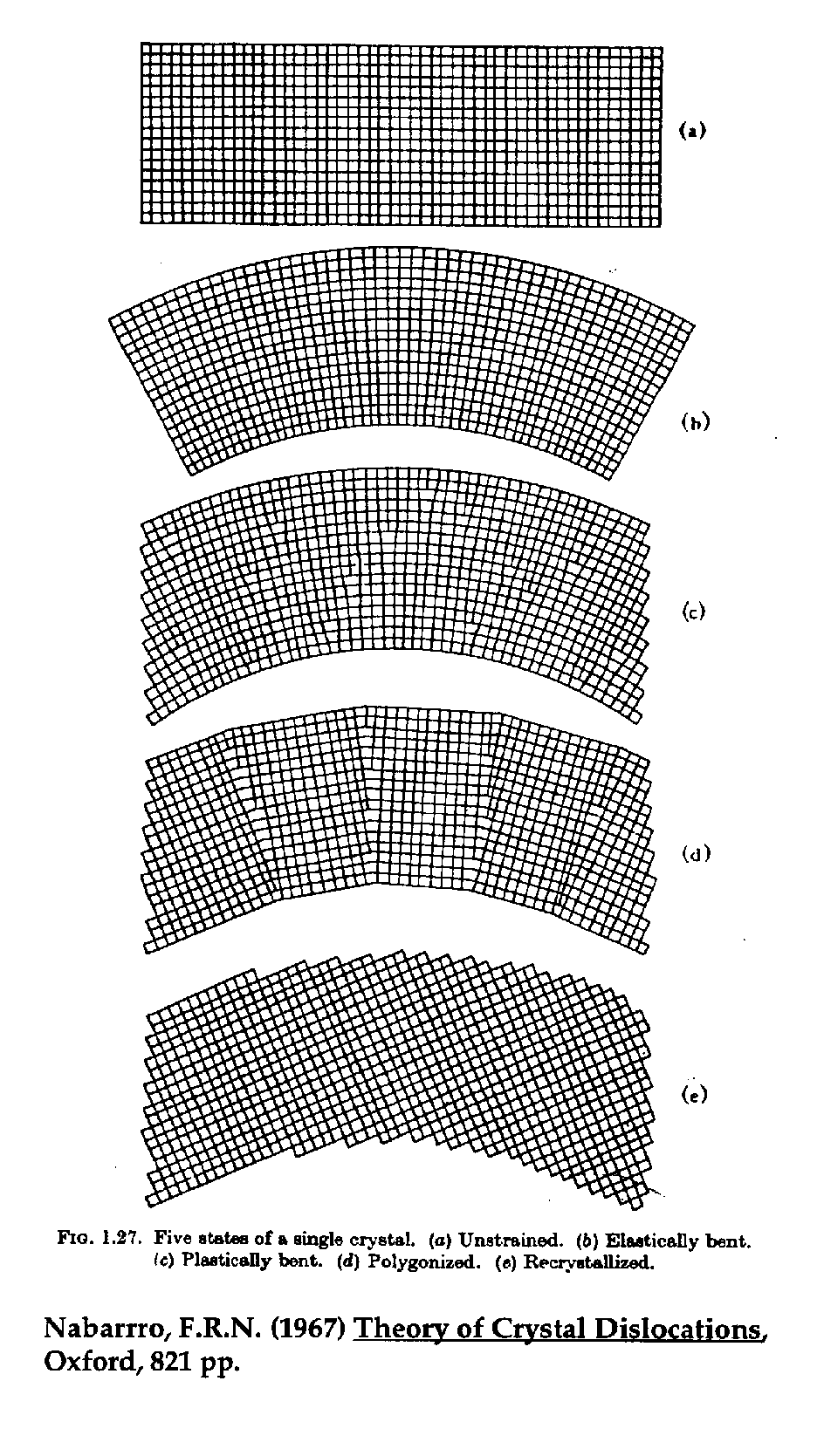
One can see that the tail of the Si Ka peak intrudes on the peak position of the Rb La line mostly due to "polygonization" of the Bragg crystals during manufacturing, which causes these extended tails (from Goldstein et al.) due to micro domain mis-orientation during the thermal cycling utilized to re-crystallize the plastically deformed Bragg crystal to improve reflectivity:
Meanwhile, here are the quant results *without* the interference correction running the SiO2 as an unknown (using standards SiO2 for Si by EDS, and RbTiOPO4 for Rb, and TiO2 for Ti using WDS):
Un 4 SiO2 as unk, Results in Elemental Weight Percents
ELEM: Rb Ti Si
TYPE: ANAL ANAL ANAL
BGDS: LIN EXP EDS
TIME: 80.00 80.00 70.00
BEAM: 49.71 49.71 49.71
ELEM: Rb Ti Si SUM
118 .148 .001 40.921 41.071
119 .156 -.002 40.989 41.143
120 .156 -.003 40.977 41.130
121 .149 -.002 40.995 41.143
122 .145 .000 40.973 41.118
AVER: .151 -.001 40.971 41.121
SDEV: .005 .002 .029 .030
SERR: .002 .001 .013
%RSD: 3.22 -143.58 .07
STDS: 1023 22 14
First of all we note that besides the interference on Rb by Si of around 1500 PPM, the totals are quite low, because although we added Si by EDS, we forgot to add oxygen by EDS. And because it's an unknown sample, the software does not know that oxygen is present. So we could either turn on oxygen by stoichiometry as seen here:
Un 4 SiO2 as unk, Results in Elemental Weight Percents
ELEM: Rb Ti Si O
TYPE: ANAL ANAL ANAL CALC
BGDS: LIN EXP EDS
TIME: 80.00 80.00 70.00 ---
BEAM: 49.71 49.71 49.71 ---
ELEM: Rb Ti Si O SUM
118 .171 .001 46.634 53.149 99.954
119 .180 -.002 46.711 53.236 100.125
120 .179 -.003 46.698 53.220 100.095
121 .172 -.002 46.718 53.244 100.133
122 .167 .000 46.692 53.215 100.075
AVER: .174 -.001 46.691 53.213 100.076
SDEV: .006 .002 .034 .038 .072
SERR: .003 .001 .015 .017
%RSD: 3.22 -143.58 .07 .07
STDS: 1023 22 14 ---
Or, we could leave it as elemental and just add oxygen by EDS using the SiO2 standard as the oxygen standard, since we acquired an EDS spectra automatically on each standard like this:
Un 4 SiO2 as unk, Results in Elemental Weight Percents
ELEM: Rb Ti Si O
TYPE: ANAL ANAL ANAL ANAL
BGDS: LIN EXP EDS EDS
TIME: 80.00 80.00 70.00 70.00
BEAM: 49.71 49.71 49.71 49.71
ELEM: Rb Ti Si O SUM
118 .171 .001 46.656 53.679 100.507
119 .180 -.002 46.745 54.002 100.925
120 .180 -.003 46.738 54.104 101.018
121 .172 -.002 46.756 54.080 101.006
122 .167 .000 46.732 54.092 100.992
AVER: .174 -.001 46.725 53.991 100.890
SDEV: .006 .002 .040 .179 .217
SERR: .003 .001 .018 .080
%RSD: 3.22 -143.58 .09 .33
STDS: 1023 22 14 14
Either way we get a decent total and more importantly as I will show below, a better matrix correction (and why would a matrix correction matter for a minor element you might ask? See below).
Now it should also be pointed out that the net intensities for Si and O by EDS were obtained from the default Thermo software profile without any special processing for background fitting or peak stripping so this is quite good actually for oxygen. Now let's turn on the interference for Rb La by Si as seen here:
 Un 4 SiO2 as unk, Results in Elemental Weight Percents
Un 4 SiO2 as unk, Results in Elemental Weight Percents
ELEM: Rb Ti Si O
TYPE: ANAL ANAL ANAL ANAL
BGDS: LIN EXP EDS EDS
TIME: 80.00 80.00 70.00 70.00
BEAM: 49.71 49.71 49.71 49.71
ELEM: Rb Ti Si O SUM
118 .002 .001 46.665 53.588 100.256
119 .012 -.002 46.754 53.911 100.674
120 .012 -.003 46.746 54.013 100.768
121 .005 -.002 46.765 53.989 100.758
122 .002 .000 46.741 54.002 100.744
AVER: .007 -.001 46.734 53.901 100.640
SDEV: .005 .002 .040 .179 .218
SERR: .002 .001 .018 .080
%RSD: 77.68 -143.58 .09 .33
STDS: 1023 22 14 14
Now that looks better! 70 PPM +/- 50 PPM (one sigma) with only 80 seconds of counting time (15 keV, 50 nA), so essentially zero. Here's another analysis of the synthetic SiO2 as an unknown, where we obtained 40 PPM +/- 30 PPM, again essentially zero:
Un 5 SiO2 as unk, Results in Elemental Weight Percents
ELEM: Rb Ti Si O
TYPE: ANAL ANAL ANAL ANAL
BGDS: LIN EXP EDS EDS
TIME: 80.00 80.00 70.00 70.00
BEAM: 50.46 50.46 50.46 50.46
ELEM: Rb Ti Si O SUM
153 .004 -.001 47.988 55.251 103.242
154 .003 .003 46.401 53.169 99.575
155 .000 -.003 46.745 53.566 100.309
157 .008 .002 47.002 54.375 101.388
AVER: .004 .001 47.034 54.090 101.128
SDEV: .003 .003 .682 .922 1.594
SERR: .002 .001 .341 .461
%RSD: 88.93 458.16 1.45 1.71
STDS: 1023 22 14 14
STKF: .3028 .5547 .4101 .2664
STCT: 5506.7 32081.8 48240.1 16388.5
UNKF: .0000 .0000 .4125 .2712
UNCT: .5 .3 48522.6 16683.3
UNBG: 41.0 45.9 .0 .0
ZCOR: 1.1959 1.2024 1.1402 1.9948
KRAW: .0001 .0000 1.0059 1.0180
PKBG: 1.01 1.01 .00 .00
INT%: -97.89 ---- ---- ----
Now here's the interesting thing about the matrix correction in this analysis. Let's go back to the Un 4 SiO2 as unk sample and this time I'll turn off the oxygen by EDS and so we obtain this result for the Rb:
Un 4 SiO2 as unk, Results in Elemental Weight Percents
ELEM: Rb Ti Si O
TYPE: ANAL ANAL ANAL ANAL
BGDS: LIN EXP EDS EDS
TIME: 80.00 80.00 70.00 ---
BEAM: 49.71 49.71 49.71 ---
ELEM: Rb Ti Si O-D SUM
118 .000 .001 40.929 --- 40.931
119 .009 -.002 40.997 --- 41.004
120 .009 -.003 40.985 --- 40.991
121 .003 -.002 41.003 --- 41.005
122 .000 .000 40.980 --- 40.980
AVER: .004 -.001 40.979 --- 40.982
SDEV: .004 .002 .029 --- .031
SERR: .002 .001 .013 ---
%RSD: 105.09 -143.58 .07 ---
STDS: 1023 22 14 ---
STKF: .3028 .5547 .4101 ---
STCT: 5490.5 32240.2 48315.1 ---
UNKF: .0000 .0000 .4098 ---
UNCT: .7 -.6 48279.9 ---
UNBG: 40.5 46.1 .0 ---
ZCOR: 1.0380 1.1985 1.0000 ---
KRAW: .0001 .0000 .9993 ---
PKBG: 1.02 .99 .00 ---
INT%: -97.25 ---- ---- ---
Notice that we obtain 40 PPM of Rb without oxygen in the matrix and also notice that the matrix correction for Rb La in this matrix is calculated as 1.038. Now we turn oxygen by EDS back on and we obtain this result:
Un 4 SiO2 as unk, Results in Elemental Weight Percents
ELEM: Rb Ti Si O
TYPE: ANAL ANAL ANAL ANAL
BGDS: LIN EXP EDS EDS
TIME: 80.00 80.00 70.00 70.00
BEAM: 49.71 49.71 49.71 49.71
ELEM: Rb Ti Si O SUM
118 .002 .001 46.665 53.588 100.256
119 .012 -.002 46.754 53.911 100.674
120 .012 -.003 46.746 54.013 100.768
121 .005 -.002 46.765 53.989 100.758
122 .002 .000 46.741 54.002 100.744
AVER: .007 -.001 46.734 53.901 100.640
SDEV: .005 .002 .040 .179 .218
SERR: .002 .001 .018 .080
%RSD: 77.68 -143.58 .09 .33
STDS: 1023 22 14 14
STKF: .3028 .5547 .4101 .2664
STCT: 5490.5 32240.2 48315.1 16364.3
UNKF: .0001 .0000 .4098 .2704
UNCT: 1.0 -.6 48279.9 16614.5
UNBG: 40.5 46.1 .0 .0
ZCOR: 1.1961 1.2024 1.1404 1.9931
KRAW: .0002 .0000 .9993 1.0153
PKBG: 1.02 .99 .00 .00
INT%: -96.25 ---- ---- ----
Now we obtain 70 PPM of Rb! Just by adding oxygen into the matrix correction we raised the Rb content (a trace element since it's probably close to zero in the synthetic SiO2), from 40 PPM to 70 PPM!
Then we were able to have the students think on this and observe that the Rb La line cannot fluoresce the Si Ka edge since the Rb La = 1.694 keV and Si K edge = 1.84 keV. But Rb La *can* fluoresce the O K edge, so Rb La is significantly more absorbed by oxygen than Si and the matrix correction goes from 1.038 to to 1.1961!