So continuing on this overview of the constant k-ratio and dead time calibration topic which started with this post here:
https://probesoftware.com/smf/index.php?topic=1466.msg11100#msg11100I thought I would re-post these plots because they very nicely demonstrate the higher accuracy of the logarithmic dead time correction expression compared to the traditional linear expression at moderate to high beam currents:
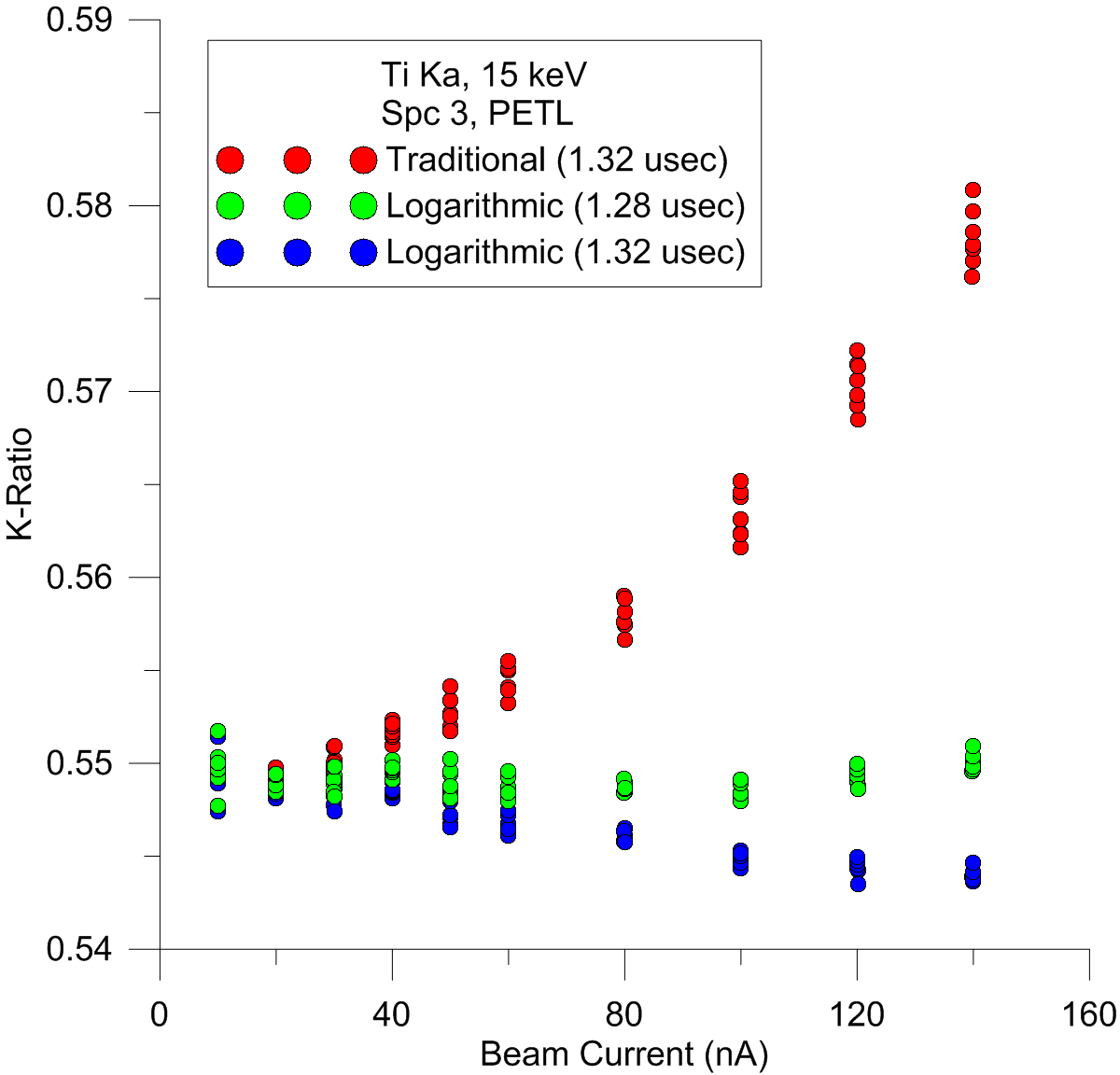
Clearly, if we want to acquire high speed quant maps or measure major, minor and trace elements together, it's pretty obvious that the new dead time expressions are going to yield more accurate results.
And if anyone still has concerns about how these the new logarithmic expression performs at low beam currents, simply examine this zoom of the above plot showing results at 10 and 20 nA:
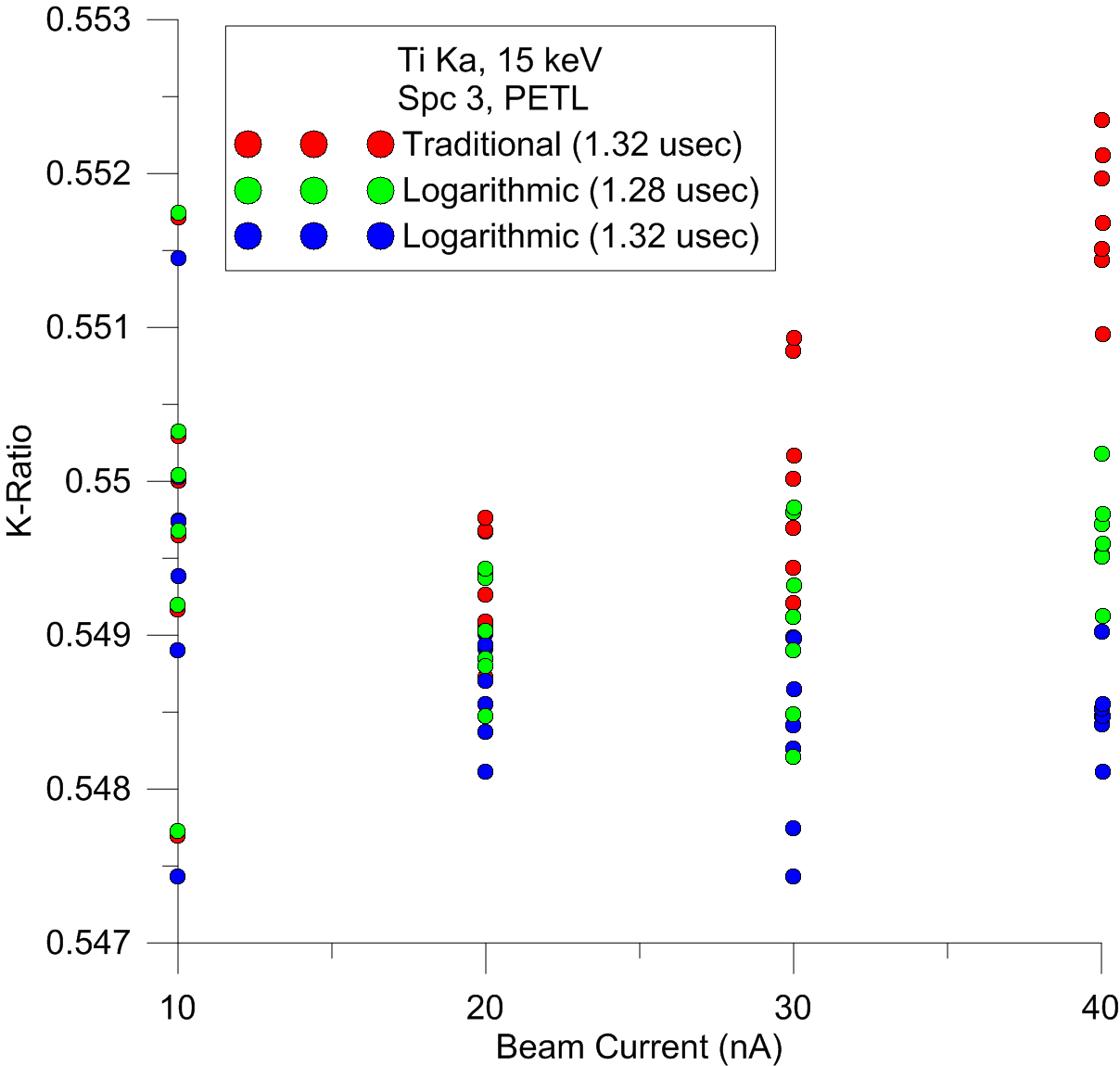
All three are statistically identical at these low beam currents! And remember, even at these relatively low count rates there are still some non-zero number of multiple photon coincidence events occurring, so we would argue that even at these low count rates, the logarithmic expression is the more accurate expression.
OK, with that out of the way, let's proceed with the promised discussion regarding SG's comments on the factors contributing towards dead time effects in WDS spectrometers, because there is no doubt that several factors are involved in these dead time effects, both in the detector itself and the electronics.
But however we measure these dead time effects by counting photons, they are all combined in our measurements, so the difficulty is in separating out these effects. But the good news is that these various effects may not all occur in the same count rate regimes.
For example, we now know from Monte Carlo modeling that at even relatively low count rates, that multiple photon coincidence events are already starting to occur. As seen in the above plot starting around 30 to 40 nA (>50K to 100K cps), on some large area Bragg crystals.
As the data reveals, the traditional dead time expression does not properly deal with these events, so that is the rationale for the multiple term expressions and finally the new logarithmic expression. So by using this new log expression we are able to achieve normal quantitative accuracy up to count rates of 300K to 400K cps (up to 140 nA in the first plot). That's approximately 10 times the count rates that we would normally limit ourselves to for quantitative work!
As for nomenclature I resist the term "pulse pileup" for WDS spectrometers because (and I discussed this with Nicholas Ritchie at NIST), to me the term implies a stoppage of the counting system as seen in EDS spectrometers.
However, in WDS spectometers we correct the dead time in software, so what we are attempting to predict are the photon coincidence events, regardless of whether they are single photon coincidence or multiple photon coincidence. And as these events are 100% due to probabilistic parameters (i.e., count rate and dead time), we merely have to anticipate this mathematically, hence the logarithmic expression.
To remind everyone, here is the traditional dead time expression which only accounts for single photon coincidence:
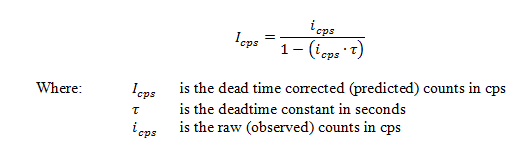
And here is the new logarithmic expression which accounts for single and multiple photon coincidences:
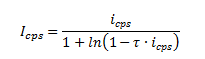
Now, what about even higher count rates, say above 400K cps? Well that is where I think SG's concerns with hardware pulse processing start to make a significant difference. And I believe we can start to see these "paralyzing" (or whatever we want to call them) effects at count rates over 400K cps (above 140 nA!) as shown here, first by plotting with the traditional dead time expression:
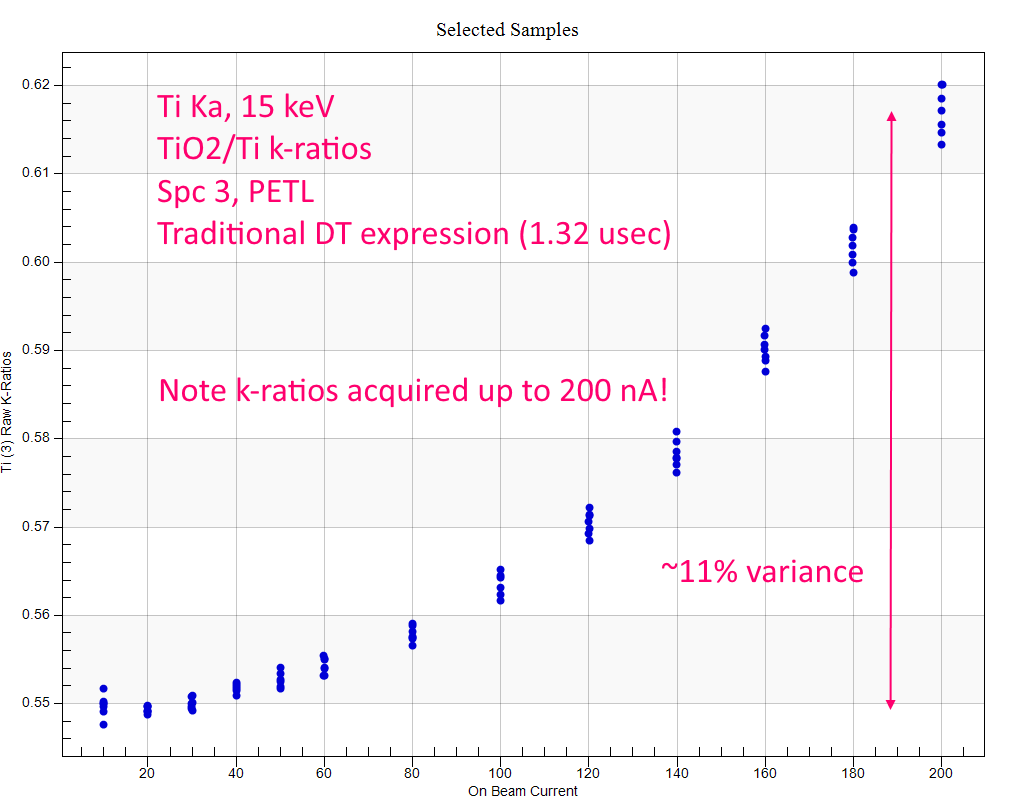
Pretty miserable accuracy starting at around 40 to 60 nA. Now the same data up to 200 nA, but using the new logarithmic expression:
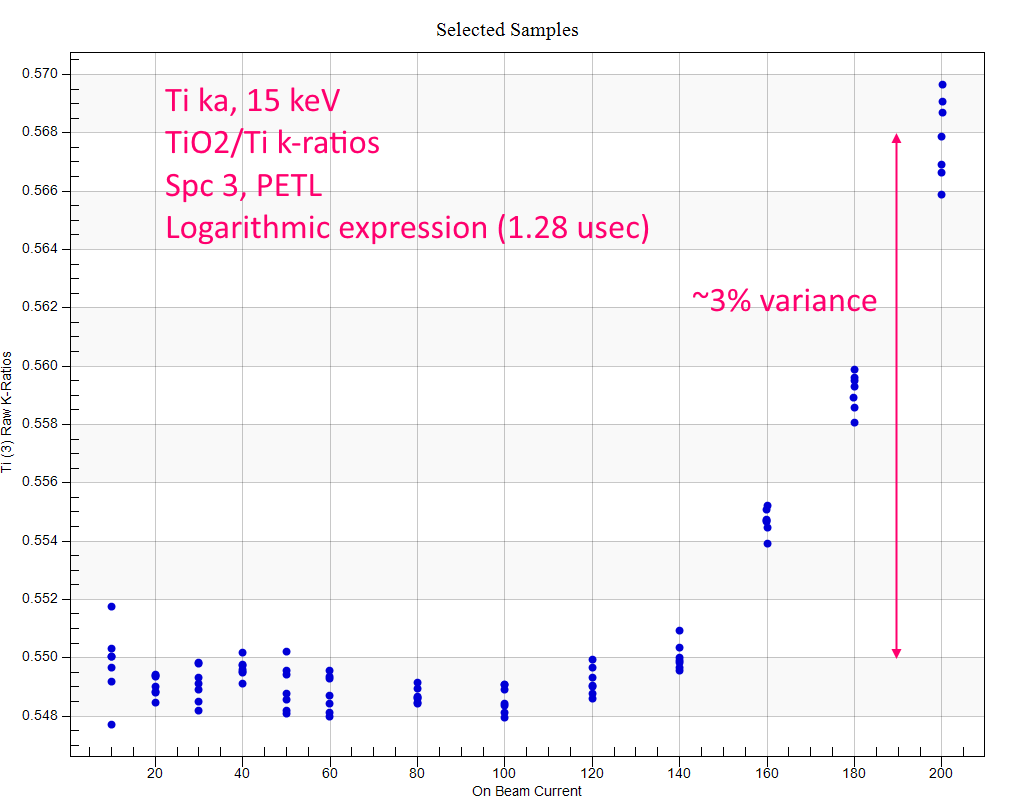
Much better obviously, but also under correcting starting about 160 nA of beam current which corresponds to a predicted count rate on Ti metal of around 450K cps!

So yeah, the logarithmic expression starts to fail at these extremely high count rates starting around 500K cps, but that's a problem we will leave to others, as we suspect these effects will be hardware (JEOL vs. Cameca) specific.
Next we'll discuss some of the other types of instrument calibration information we can obtain from these constant k-ratio data sets.