Something is happening above 500K cps. Try the Heinrich linear method at count rates over 500K cps and let us know what you see.
It's clear to me at least that the additional terms of the Taylor expansion series in the dead time correction have an enormous benefit in allowing us to maintain constant k-ratios over a much larger range of count rates (beam currents) than before. This is particularly important for new instruments with large area Bragg crystals that can easily attain these 100K cps count rates at moderate conditions.
Yes, I’m aware that the linear model will not produce useful results at high count rate (> several tens kcps).
Well that's sort of the point of this topic! To reiterate:
1. Using the constant k-ratio method we can acquire k-ratios that allow us to determine the dead time constants for each spectrometer (and each crystal energy range if desired).
2. We can display the same k-ratio data using a primary standard measured at a single beam current to determine the accuracy of our picoammeter calibration.
3. We can plot k-ratios from multiple spectrometers so we can compare the effective takeoff angles of each of our spectrometers/crystals to determine our ultimate quantitative accuracy.
4. And finally, using the expanded dead time correction expression, we can correct WDS intensities at count rates up to around 500k cps with accuracy not previously possible.
Your uncorrected data are difficult to interpret in part because both the primary and secondary standards require large, non-linear dead time corrections that lead to a roughly linear appearance of the uncorrected plot of k-ratio versus current. You also haven’t presented peak searches or wavelength scans so that peak shapes can be compared at increasing count rates.
This is what you keep saying but I really don't think you have thought this through. There is nothing non-linear about the expanded dead time correction. The dead time expression (all of them) are merely a logical mathematical description of the probability of two photons entering the detector within a certain period of time.
The traditional dead time expression, by utilizing only a single term of this Taylor expansion series, is simply a very crude approximation of this probability, and therefore is only accurate for count rates up to around 50K cps. Though it depends on the actual dead time, so Cameca instruments with roughly 3 usec dead times and using the traditional expression are probably only accurate up to 50K cps. While JEOL instruments with dead times around 1.5 usec, may be able to get up to ~80K cps with the traditional expression, as you have shown.
As Willis pointed out in 1993, by utilizing a second term in the dead time expression one can obtain better precision in this probability estimate, and we find that one can get up to count rates around 100K cps or so before the wheels come off. Maybe a little higher on a JEOL with shorter dead times.
But by utilizing an additional (4) terms of this probability series, we can now get high accuracy k-ratios up to count rates close to 500K cps. It's just math.
As far as the effects of peak shapes go at these high currents, I would have thought that the k-ratio data speaks for itself! But I remember now that I did do a screen capture of the PHA peak shapes looking at Mn Ka on Mn metal at 200 nA last week:
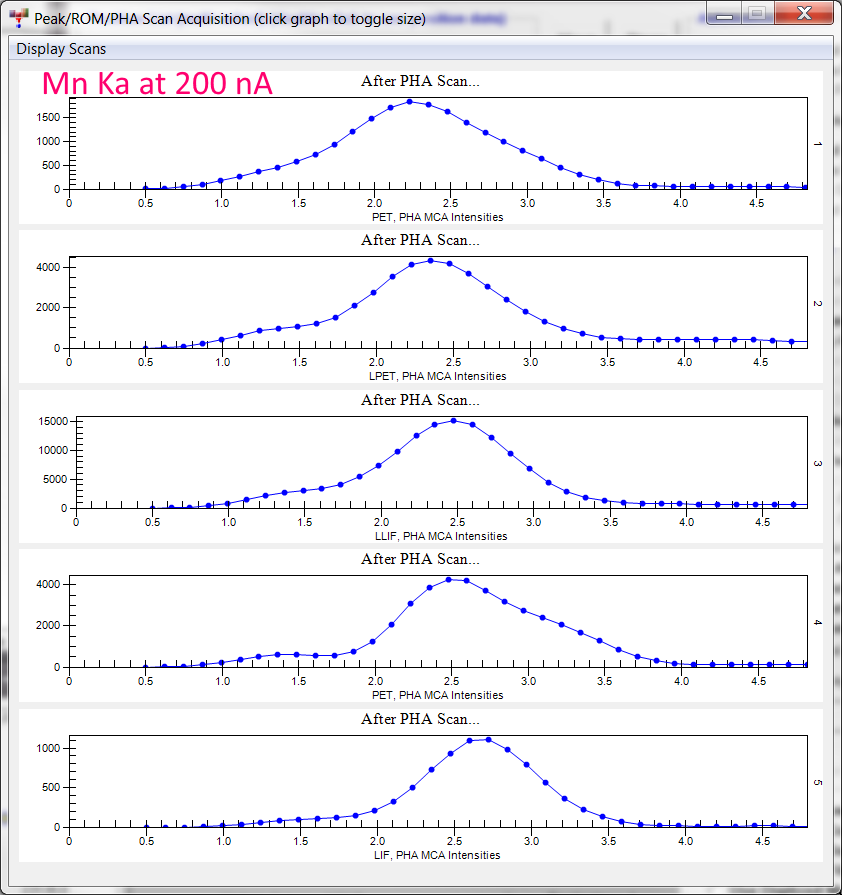
The LPET count rates were over 240K cps at 200 nA. Surprisingly good I think for an instrument with 3 usec dead times! I'll try and remember to do a wavescan at 200 nA next time I'm in the lab, but again, the accuracy of the k-ratio data tells me that we are able to perform quantitative analysis at count rates never before attainable.
If the counter is nearing paralysis, then, obviously, the Ti Ka count rate on Ti metal will produce this effect at lower current than TiO2. This would be manifested as increasing positive deviation from rough linearity at high current on the plot of k-ratio versus current. If I put a ruler up to your plot, then I can in fact see the apparent k-ratio deviating in this manner (but I need a ruler to see it).
When dealing with these high count rates, it really is necessary to specify whether the stated count rate is corrected or not (like the 506 kcps on Ti metal at 180 nA); this is one advantage of plotting against specified measured or corrected count rate rather than current. On my channel 2/PETL, I see no obvious evidence for paralysis at 200 nA when measuring Ti Ka on high-purity TiO2 (with measured count rate between 250 and 300 kcps). When I do a peak search at 400 nA to simulate the count rate on Ti metal, I get a peak with a distinctly flat top, indicating onset of paralysis.
Considering the above, it appears likely that your k-ratios collected above 140 nA are in fact affected by abnormal counter behavior, and so my first impression of the uncorrected ratios was wrong. (But who could blame me considering that your plot contains no explicit information on measured count rate?) What bothers me about your k-ratio versus current plots, though, is the fact that I can see patterns in the corrected values. For instance, why do the corrected ratios for Anette’s channels 2 and 3 decrease in similar fashion when progressing from about 40 to 100 nA? Why does a maximum appear to occur at 40 nA for the corrected channel 5 ratios?
I think that you need to investigate your model further to see if it is producing unphysical behavior. I’ve already pointed out a potential problem on my N12/N32 versus N12 plot for Ti (shown again below). It is absolutely physically impossible for N12/N32 to fall below the ratio determined in my linear fit, as this fit gives the extrapolation to zero count rate (noting that I collected abundant data in the linear region). You or somebody else absolutely needs to test the higher order models in the same fashion. Forming a ratio of Ti Ka and Ti Kb (with Kb measured on a spectrometer that produces relatively low count rate) is especially useful because the Kb count rate can be corrected reasonably with the linear model. If you want to stick with k-ratios, then use a secondary standard that doesn’t contain much of the element under consideration (like Fe in bornite, Cu5FeS4, while using Fe metal as the primary standard). On my plot of the uncorrected or linearly corrected data, note that no obvious deviation from linearity occurs below 85 kcps.
Well I'm glad you now see it. And thank-you for taking the time to debate this with me. I have to say, all of this argument has actually helped me to appreciate exactly how good this new method and expression are.
The small deviations you point out are interesting and perhaps will provide additional insight into the inner workings of our instruments, but it should be noted that they are in the sub 1% level and significantly smaller than the k-ratio variations from one spectrometer to another. The fact that we can attain 1% k-ratio accuracy up to 500K cps is, to me at least and Anette as well, the take home message in my book.
Here's an idea: I can't send you Anette's data until I ask her, but perhaps your best bet for understanding this constant k-ratio method and the new dead time expression is to perform a constant k-ratio run yourself.
You already own Probe for EPMA, so why don't you just fire it up, go to the Help menu and update it to the latest version so you have the new dead time expression. Then using Ti metal and TiO2, or any two materials with a large difference in count rates, try it out on your PET and LIF crystals. Do you have any large area crystals? That is where these effects will be most pronounced. The procedure has been fully documented and is attached below.
Remember, Probe for EPMA has the traditional (single term) expression, the Willis (two term) expression, and the new six term expression, all available with a click of the mouse. They are each simply more precise formulations of the probability calculation of randomly overlapping time intervals.
And by unchecking the Use Dead Time Correction checkbox you can even turn off the dead time correction completely!
With the latest version of Probe for EPMA, it just takes a few minutes to set up a completely automated overnight run using the multiple sample setups feature with different beam currents. See the attached PDF document for complete details.
Edit by John: updated pdf attachment