New method for calibration of dead times (and picoammeter)

[Probeman]

So there remains the question of emission line energies and dead time calibration.

I will run some more measurements this weekend, but it may simply be the case that Cameca instruments, with their "enforced" integer dead time electronics do not experience variable pulse widths as a function of emission line energies.

In the mean time it would be most helpful if we could obtain additional constant k-ratio measurements from other instruments, particularly JEOL instruments.

[Probeman]

So I used the same dead time constants from the last Sunday run and applied them to the Monday run where I acquired more beam currents but only up to 100 nA and everything looked very stable and consistant using the "super high precision" dead time correction expression (with six terms).







You get the picture...  again we see the "glitch" at around 40 nA, but the k-ratios are quite constant from 6 to 100 nA.

[John Donovan]

Does anyone know what dead time expressions Cameca and JEOL are using for their WDS intensities?  Or Bruker and Thermo WDS?

By the way, we wrote up the complete procedure for running the constant k-ratio test and re-processing the data, and it is attached below (login to see attachments as usual).

Let us know if the document is unclear at any point.

Edit by John: update pdf attachment for standard intensity drift correction notes.

[Probeman]

I ran different elements (emission energies) on the instrument yesterday to see if I could tease out any trends (or not) in the dead time calibrations using the new "super high precision" dead time correction expression. Unfortunately I didn't think to keep the bias voltages exactly the same on all spectrometers so that is a possible variable not controlled for.  But the initial data is still worth examining I think.

Here is the run I did on 05/29/2022 up to 200 nA using Zn Ka, Se La and Te La at 8.64, 1.38 and 3.77 keV respectively:
                 1            2            3           4            5
              Te La     Se La     Zn Ka     Te La     Zn Ka
               PET       LTAP       LLIF        PET        LIF
BIAS    1320v     1330v     1850v     1340v     1840v
DT      2.85us    2.80us    2.80us    3.00us    3.00us

When I plotted up the new data from 06/04/2022 using the sample DT constants from 05/29/2022 I saw some significant differences, for example on Sp 1 when going from Te La (PET) to Se La (TAP) and using the same bias voltages the k-ratio plot looks like this:



After the DT is adjusted to 3.30 used, in order to produce a more constant k-ratio, we obtain this:



So here is a summary of the run from yesterday using different emission lines on the spectrometers and adjusted to obtain a constant k-ratio as a function of beam current:

                 1            2           3            4            5
              Se La     Te La     Te La     Se La     Te La
               TAP       LPET       LPET        TAP        PET
BIAS    1320v     1320v     1850v     1313v     1850v
DT      3.30us    2.60us    2.70us    3.20us    2.90us

The bias voltages is red were modified from the previous run (note that Sp 3 and Sp 5 are 2 atm detectors). So, you can see that going from Te La (PET) to SE La (TAP) on sp 1 and 4 the emission energy went down, but the DT required for a constant k-ratio went up (both low pressure detectors).

However, on Sp 3 and 5, going from Zn Ka (LIF) to Te La (PET), the emission energies also went down, but the DT had to be adjusted down slightly (by 0.1 usec), to obtain a constant k-ratio. But both of these were 2 atm detectors, so that is another variable.

Meanwhile on Sp 2 going from Se La (TAP) to Te La (PET) the emission energy went up, but the DT had to be adjusted down slightly to obtain a constant k-ratio.

A bit of a mixed bag to say the least, so I am going to try some other emission lines this weekend.  By the way, I heard back from Cameca and they only utilize the "normal" or classic dead time expression, which we now know will not work above 50K cps.

In any case, one can specify different dead time constants for different crystals in Probe for EPMA, so maybe this variation in DT is something that can be dealt with.

[John Donovan]

Does anyone know what dead time expressions Cameca and JEOL are using for their WDS intensities?  Or Bruker and Thermo WDS?

By the way, we wrote up the complete procedure for running the constant k-ratio test and re-processing the data, and it is attached below (login to see attachments as usual).

Let us know if the document is unclear at any point.

We added a final section to the above pdf document attached to this message:

https://probesoftware.com/smf/index.php?topic=1466.msg10920#msg10920

Describing how to edit your SCALERS.DAT file once you have determined your new dead time constants using the "super high precision" expression.

[Probeman]

OK, so this is pretty cool.

It just occurred to me last night (yes I was dreaming about WDS!), that these "constant k-ratio" measurements can characterize not only our dead time constants and our picoammeter calibrations, but also our "effective" takeoff angles! The effective takeoff angle being the actual angle of X-ray measurement defined by our Bragg crystal (is it symmetrically diffracting?) and the spectrometer alignment and the surface of our sample holder. Of course, this requires that one measures the same element and x-ray line on more than one spectrometer!

So the reason this "constant k-ratio" method is interesting is not only because we should we get the same k-ratio at any beam current, but we should also get the same k-ratios (within precision) for *all* the spectrometers on our instrument, assuming of course the same element, X-ray line, beam energy and takeoff angle are utilized in the k-ratio measurement.

This is exactly the "simultaneous k-ratio" test that is often utilized in initial instrument acceptance testing:

https://probesoftware.com/smf/index.php?topic=369.msg1948#msg1948

So here is a "constant k-ratio" plot of the two spectrometers using the same (Se La) emission line measured on two spectrometers using TAP crystals:



As you can see spectrometers 1 and 4 agree pretty well with each other, which is impressive because the Se La line is only 1.38 keV, so fairly low energy and therefore more affected by variations in the effective takeoff angle.  Now how about Te La on three spectrometers using PET crystals:



Hmmm, seems we might have a small difference between the two LPET crystals and the normal PET crystal.  The cool thing about using the constant k-ratio method for this simultaneous k-ratio evaluation is that one can obtain an immediate sense of the relative accuracy of the error. Our investigations continue...

I guess the point is that we need to make sure we have consistent k-ratios not only for different beam currents (dead times and picoammeter) but also between our spectrometers, before we start comparing our k-ratios to other instruments (which are hopefully equally well calibrated in these parameters!).

[John Donovan]

Does anyone know what dead time expressions Cameca and JEOL are using for their WDS intensities?  Or Bruker and Thermo WDS?

By the way, we wrote up the complete procedure for running the constant k-ratio test and re-processing the data, and it is attached below (login to see attachments as usual).

Let us know if the document is unclear at any point.

We added a final section to the above pdf document attached to this message:

https://probesoftware.com/smf/index.php?topic=1466.msg10920#msg10920

Describing how to edit your SCALERS.DAT file once you have determined your new dead time constants using the "super high precision" expression.

We added yet another section to the constant k-ratio method procedure on simultaneous k-ratios in the pdf attached here.

Edit by John: update pdf attachment

[Brian Joy]

I'd like to point out that the (simple) expression for deadtime commonly in use, N’/I = k(1-N’τ), and lending itself to illustration on plots of cps/nA versus cps, is not the only means of calculating deadtime (simply).  Heinrich et al. (1966; attached) applied the so-called “ratio method,” in which the ratios of the observed count rates (N1’ and N2’) of two X-ray lines (they used Cu Ka and Cu Kb on Cu metal) measured simultaneously on two spectrometers at varying beam current (to produce two datasets in which N1’ alternately represents Cu Ka or Cu Kb) are used to determine the deadtimes for both spectrometers.  Although the expressions are linear and only applicable at relatively low count rates, since evaluation of the deadtime by this means only involves consideration of slopes and intercepts on plots of N1’/N2’ versus N1’ (Figs. 7 and 8 ), inaccuracy in the beam current measurement is irrelevant.

[sem-geologist]

This thread made me sit few days on SX100 and do some checking.
The production of some plots and consolidating the data will take some time.

However at this moment with 100% being sure I can point to few problems of non-linearity:
1. Widely used and evangelized here in this forums differential PHA mode with wide-window (differently to integral method) will introduce non linearity at high count rates, as PHA "peaks" of double and triple pulse-pileups will cross into/move into the PHA window. That makes counting particularly prone to be affected by random fluctuations of temperature and pressure. Better would be to use integral (simpler), or narrow (moving with the peak) window. The second one would have pseudo-expandable dead time behavior. The count rate between integral and wide-window PHA drops down to 95% at worst case. I see absolutely no advantage of wide window vs integral, as integral will have simple parabola shape in beam_current vs intensity plot, where wide-window PHA will have similar parabola with distortions (waves) at high current. Plots in this method thread does not catch that as jumps from 140 to 200 without smaller steps in between.
2. This proposed factorial math model does not work well. In case the higher count rate is fitted correctly - the lower count rate is the overestimated. In particularly if ignoring point one, it can produce wrong fitting for both high and low currents.
3. 2nd point is baseless claim? How to explain those dead time of 2.9 us while hardware blanks pulses for 3us. Unless this SX100 is accelerated to relativistic speeds or it have a Black Hole under there is no physical way for pulses be passed before unblanking. It rather evidences over fitting of that method at low currents (actually at low count rates, we should not care about beam current at all), where count rates are overestimated. I already had shared the jupyter notebooks with MC simulation in some other thread. There It was clear that that formula overestimates the rate at low count rate.

[Probeman]

I'd like to point out that the (simple) expression for deadtime commonly in use, N’/I = k(1-N’τ), and lending itself to illustration on plots of cps/nA versus cps, is not the only means of calculating deadtime (simply).  Heinrich et al. (1966; attached) applied the so-called “ratio method,” in which the ratios of the observed count rates (N1’ and N2’) of two X-ray lines (they used Cu Ka and Cu Kb on Cu metal) measured simultaneously on two spectrometers at varying beam current (to produce two datasets in which N1’ alternately represents Cu Ka or Cu Kb) are used to determine the deadtimes for both spectrometers.  Although the expressions are linear and only applicable at relatively low count rates, since evaluation of the deadtime by this means only involves consideration of slopes and intercepts on plots of N1’/N2’ versus N1’ (Figs. 7 and 8 ), inaccuracy in the beam current measurement is irrelevant.

Hi Brian,
I saw your post last night and was planning on responding this morning and when I got up to do so, your post has been removed and replaced with the above post.  I was so looking forward to responding to your previous comments.  Your feedback is always appreciated even when we're not in complete agreement!

Just working from memory I would just explain that with regards to your comment on simultaneous k-ratio measurements, you are correct, one should measure k-ratios on all 5 spectrometers and we did so, but just not using the same lines. The reason being because this topic started out looking at a new method to calibrate dead times using soft x-rays (Al Ka and Mg Ka) and because of issues with beam damage and subsequent curiosity in evaluating the effects from different emission energies, we had quickly moved to looking at Zn Ka, Se La and Te La on more electrically conducting materials

However, now that the software has been improved to completely automate the acquisition of these "constant k-ratio" datasets (with a y-axis stage increment for each beam current sample setup), yesterday we acquired some additional data sets, specifically Ti Ka on all 5 spectrometers.  Here is using Ti metal as the primary standard and TiO2 as the secondary standard over a range of beam currents.



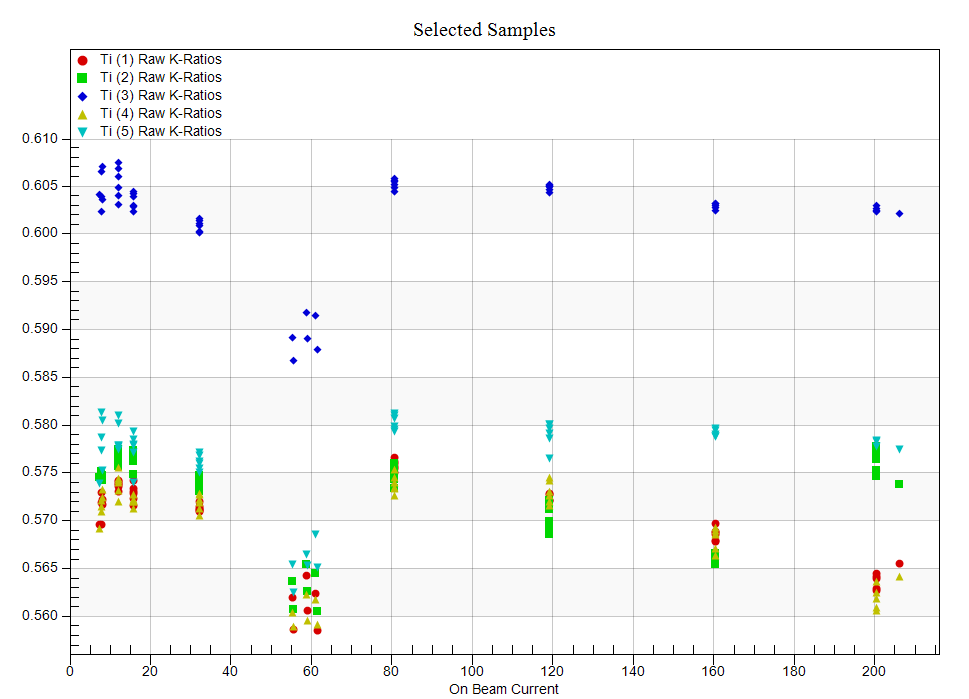
These k-ratios were calculated using the *same* dead time constants from the Zn, Se and Te calibration runs which is pretty good confirmation that emission energy doesn't seem to be a big factor in dead time. At least for Cameca instruments.  Unfortunately we still have no data from any instruments other than the Oregon instrument, but I am very much looking forward to seeing data from other instruments, especially JEOL instruments. 

The reason I think that different emission energies *might* affect JEOL instruments more  (mainly based on reports years ago from Paul Carpenter on his 8200 instrument), is that Cameca uses an "enforced" dead time circuit that forces all pulses to some integer value duration, say 3 usec. This circuit does not force the pulse width exactly to that value, hence the reason why the Cameca software includes a non-integer tweak to the software dead time correction.  In any case this electronic feature might help keep the pulse widths more consistent as a function of emission line energy.

Please note that one can see several artifacts in the above constant k-ratio plot.  The first is the anomaly at 60 nA.  It's interesting as we avoided performing any measurements around 40 nA because we had been seeing a similar anomaly. However it seems to also appear at 60 nA, perhaps when time the picoammeter range switches from the 5 to 50 nA to the 50 to 500 nA range?  We should perhaps try some measurements going from high beam currents to low beam currents.

Note also that spectrometer 3 using a LLIF Bragg crystal seems to yield significantly different k-ratios (by a couple of percent) than the other spectrometers, including a normal LiF Bragg crystal on spectrometer 5. I suspect that spectrometer 3 has some alignment issues which is interesting since we have just had a maintenance performed by Cameca, but perhaps the problem is asymmetrical Bragg diffraction. The large area crystals do seem to be more susceptible to these sorts of artifacts.

On the Heinrich paper, I had not seen this method before, thanks for sharing that.  I will definitely give that a try. With these recent Probe for EPMA software features (running multiple setup automatically one at a time and implementing a y stage axis bump for each sample setup) this is now a very easy thing to do.  I hope you also will "fire up" PFE with this new "super high precision" dead time expression and see what you obtain on your instrument for these constant k-ratio measurements.

In your previous comment you also mentioned your concerns with making one adjustment for separate calibration issues and I agree completely. Maybe you missed my earlier discussion of that very point where I said that I have concerns with making one adjustment for dead time calibration and picoammeter linearity. But it soon became clear after some experimentation, that adjusting the dead time constant (to improve the consistency of k-ratios over a large range of beam current), did not actually remove the picoammeter miscalibrations, it just made them much more clearly visible.  See this post for that data:

https://probesoftware.com/smf/index.php?topic=1466.msg10912#msg10912

So in the above post, the first plot (in the quotation area) is the constant k-ratio plot showing some small anomalies after the dead time has been adjusted to yield the most consistent k-ratios over the range of beam current for each spectrometer.

What is interesting are the following *on-peak* intensity plots (also DT corrected) of the different spectrometers all showing the same variation which seems to be related to the different picoammeter ranges (the cps/nA intensity offset occurring on all spectrometers at around 40 nA).  I find that very interesting and suggests to me that our picoammeter ranges require some adjustment.  The only time one might be compensating for picoammeter miscalibration using this dead time adjustment is if the picoammeter was non-linear in a very linear manner!   But that would also occur for the traditional dead time calibration method using a single material (and single emission line).

As for the more recent simultaneous k-ratio observations those are simply a nice side benefit of these constant k-ratio measurements. And unsurprisingly these simultaneous k-ratio offsets seem to be very consistent over the range of beam currents just as one would expect from a spectrometer/crystal alignment/effective takeoff angle issue(s).

I am really stoked at how useful these constant k-ratio measurements seem to be and I really love how by using k-ratio units we obtain very intuitive plots of the thing we actually care about in our instrument performance, that is: k-ratios!  I look forward to measurements from your JEOL instrument.

[Probeman]

This thread made me sit few days on SX100 and do some checking.
The production of some plots and consolidating the data will take some time.

However at this moment with 100% being sure I can point to few problems of non-linearity:
1. Widely used and evangelized here in this forums differential PHA mode with wide-window (differently to integral method) will introduce non linearity at high count rates, as PHA "peaks" of double and triple pulse-pileups will cross into/move into the PHA window. That makes counting particularly prone to be affected by random fluctuations of temperature and pressure. Better would be to use integral (simpler), or narrow (moving with the peak) window. The second one would have pseudo-expandable dead time behavior. The count rate between integral and wide-window PHA drops down to 95% at worst case. I see absolutely no advantage of wide window vs integral, as integral will have simple parabola shape in beam_current vs intensity plot, where wide-window PHA will have similar parabola with distortions (waves) at high current. Plots in this method thread does not catch that as jumps from 140 to 200 without smaller steps in between.

Hi SG,
Looking forward to your data!   Hopefully you can also utilize this new "super high precision" dead time expression. I found that using the traditional expression rapidly fails above 50K cps. See here for an example:

https://probesoftware.com/smf/index.php?topic=1466.msg10909#msg10909

I also actually agree with your admonition of not using differential mode for these high current k-ratio measurements.  All the constant k-ratio measurements I have done for the last few weeks are using integral mode always.

2. This proposed factorial math model does not work well. In case the higher count rate is fitted correctly - the lower count rate is the overestimated. In particularly if ignoring point one, it can produce wrong fitting for both high and low currents.

OK, here we can disagree and the data I have supports this.  As for the math, you must have made a mistake in your calculations because the dead time correction is a simple probability calculation, and the Taylor Expansion series rigorously describes these probabilities.  As you can see from the most recent data in the plot above in my response to Brian, the lower beam current k-ratios seem to be very much in agreement with each other.  What sort of issues are you seeing on your instrument? 

And here is a plot also from yesterday showing the k-ratio for Ti metal as primary standard and SrTiO3 as a secondary standard, again showing the consistency in the k-ratios at lower beam currents, again using the "super high precision" expression:



Doesn't seem to be hurting the lower count rates to my eye. The traditional dead time expression seems to start failing even at moderate beam currents on my LPET using Ti Ka for example.

3. 2nd point is baseless claim? How to explain those dead time of 2.9 us while hardware blanks pulses for 3us. Unless this SX100 is accelerated to relativistic speeds or it have a Black Hole under there is no physical way for pulses be passed before unblanking. It rather evidences over fitting of that method at low currents (actually at low count rates, we should not care about beam current at all), where count rates are overestimated. I already had shared the jupyter notebooks with MC simulation in some other thread. There It was clear that that formula overestimates the rate at low count rate.

Well there must be a black hole underneath my instrument as it's not at all clear to me.   

I would simply attribute these values being slightly less than exactly 3 usec to the fact that electronics itself can be miscalibrated.  Simply put: how do we know these "blanking" pulses are *exactly* 3 usec?  Knowing nothing about the electronic details I might ask: exactly how good are those resistor values?  I suspect it is possible they might be a little more or a little less than the specified integer dead times.  The dead time calibration simply measures this nominal enforced pulse width empirically.

Let's do an experiment. Here is the k-ratios for spec 1 PET looking at Ti Ka using the "empirically" found dead time of 2.85 usec:



Looks OK, but clearly as pointed out previously there may be some picoammeter adjustments necessary based on the simple count rate plots in previous posts.  Now let's change it to 3.0 usec as you suggest:



Well that definitely looks worse to my eye.  Forgive me but I guess my instrument has a black hole underneath it!   And now let's try the traditional dead time expression with 3 usec:



Now that's even worse than before.  I'm not saying this is all figured out, that's why more data from more instruments would be helpful. Let's see some constant k-ratio data from your instrument.  Here's mine again using the "super high precision" Taylor Series expansion expression for DT correction:

[Probeman]

So here's a very different use case of the constant k-ratio method acquired by Ying Yu at University of Queensland.

She has an old JEOL 8200 which doesn't have any large area crystals and of course JEOL dead time constants tend to be around half of Cameca's so that's another advantage.

So here is a data set using Cu ka on CuFeS2, and Cu metal as the primary standard, on LIF going up to 120 nA using the traditional dead time expression:



Pretty constant I'd say. It helps that her DT constants are around only 1.5 usec.  And here is the same data but plotted using the super high precision dead time expression:



If you look very closely one can see that the data points on the right at the highest beam currents are very slightly lower.  How is this possible?  Well even at 120 nA on pure Cu, she's only getting around 30K cps of Cu Ka!

So in this case of an old JEOL instrument with very low count rates, the normal (traditional) dead time expression is good enough. 

To re-iterate, at dead times from 1 to 2 usec I would expect the traditional (normal) single term expression to be good to around 50K cps. Though Cameca instruments with dead times around 3 usec, might benefit from the two term high precision expression.

However, over 50K cps the high precision (two term) expression should perform better, and at over 100K cps, the super high precision (multi-term) expression will probably be necessary.  I guess the bottom line is that no matter what your count rates are, the multi-term "super high precision" dead time expression won't hurt, and in many cases (large area crystals and/or higher beam currents and/or maybe Cameca instruments in general), it will definitely help!

I'd be very interested in additional constant k-ratio measurements from any one willing to do some of these measurements.  The latest instructions for acquiring constant k-ratios are attached below.

Edit by John: updated pdf attachment

[Probeman]

In the above post, we showed data from Ying Yu's lab which demonstrated no change in intensities between using the normal (traditional) dead time expression and the "super high precision" dead time expression at low to moderate beam currents, and only the slightest intensity differences at high beam currents.

This is due to the fact that her instrument is only producing ~30k cps on pure Cu and pure Fe metal even at 120 nA beam current!  So for her instrument with its 1.45 usec dead times, the traditional dead time expression is more than sufficient. Though of course it doesn't hurt to utilize the "super high precision" dead time expression as the default (maybe they will utilize beam currents of 200 nA at some point).

Meanwhile on our SX100 instrument we remeasured Ti on Ti metal, TiO2 and SrTiO3 up to 200 nA *and* also we acquired an EDS spectrum with each data point using our Thermo Pathfinder EDS spectrometer (10 sq. mm). At 200 nA this results in ~220K cps on our PET crystals, ~600K cps (!) on our LPET crystal and ~360K cps on our EDS detector.   And please note, for the Ti Ka by EDS, the ~360K cps is not the whole spectrum count rate, it's merely the Ti ka *net intensity* count rate!   

The results for all 5 WDS spectrometers using the "super high precision" dead time expression, and also the EDS detector (of course the EDS detector is correcting for dead time losses using hardware), can be seen here:



The WDS spectrometers all look good (though with a bit of an possible asymmetrical diffraction outlier with the LLIF crystal on spec 3), and most impressively, the EDS detector did quite well up until around 200 nA, when the "wheels start to come off" around 85% DT.

[Probeman]

This is insane.  Here are quant calculations using the "super high precision" dead time expression on the most recent data set where I measured Ti Ka on Ti metal, TiO2 and SrTiO3.

Note that the absolute value of the k-ratio does not matter for this "constant k-ratio" dead time calibration method. The only thing we care is that the k-ratio remains constant as a function of beam current.

Also, for quantification I've utilized the "aggregate" feature in Probe for EPMA to combine the Ti ka intensities from all 5 spectrometers, because the matrix would be non-physical if Ti intensities from 5 spectrometers were added to the specified strontium and oxygen concentrations during the matrix iteration.

So here is Ti Ka measured on 5 spectrometers, using Ti metal as a primary standard measured at 12 nA, and TiO2 measured as a secondary standard measured at 200 nA:

St   22 Set   9 TiO2 synthetic, Results in Elemental Weight Percents
 
ELEM:       Ti      Ti      Ti      Ti      Ti       O
TYPE:     ANAL    ANAL    ANAL    ANAL    ANAL    SPEC
BGDS:      EXP     EXP     LIN     EXP     LIN
TIME:    60.00     .00     .00     .00     .00     ---
BEAM:   201.36     .00     .00     .00     .00     ---
AGGR:        5                                     ---

ELEM:       Ti      Ti      Ti      Ti      Ti       O   SUM 
XRAY:     (ka)    (ka)    (ka)    (ka)    (ka)      ()
   247  60.140    .000    .000    .000    .000  40.050 100.190
   248  60.148    .000    .000    .000    .000  40.050 100.198
   249  60.121    .000    .000    .000    .000  40.050 100.171
   250  60.137    .000    .000    .000    .000  40.050 100.187
   251  60.084    .000    .000    .000    .000  40.050 100.134
   252  60.088    .000    .000    .000    .000  40.050 100.138

AVER:   60.120    .000    .000    .000    .000  40.050 100.170
SDEV:     .027    .000    .000    .000    .000    .000    .027
SERR:     .011    .000    .000    .000    .000    .000
%RSD:      .05   .0000   .0000   .0000   .0000     .00

PUBL:   59.939    n.a.    n.a.    n.a.    n.a.  40.050  99.989
%VAR:      .30     .00     .00     .00     .00     .00
DIFF:     .181     ---     ---     ---     ---    .000
STDS:      522       0       0       0       0     ---

and here is SrTiO3 again using Ti metal as a primary standard measured at 12 nA, and SrTiO3 measured as a secondary standard measured at 200 nA:

St  251 Set   9 Strontium titanate (SrTiO3), Results in Elemental Weight Percents
 
ELEM:       Ti      Ti      Ti      Ti      Ti      Sr       O
TYPE:     ANAL    ANAL    ANAL    ANAL    ANAL    SPEC    SPEC
BGDS:      EXP     EXP     LIN     EXP     LIN
TIME:    60.00     .00     .00     .00     .00     ---     ---
BEAM:   200.42     .00     .00     .00     .00     ---     ---
AGGR:        5                                     ---     ---

ELEM:       Ti      Ti      Ti      Ti      Ti      Sr       O   SUM 
XRAY:     (ka)    (ka)    (ka)    (ka)    (ka)      ()      ()
   253  26.226    .000    .000    .000    .000  47.742  26.154 100.122
   254  26.244    .000    .000    .000    .000  47.742  26.154 100.140
   255  26.228    .000    .000    .000    .000  47.742  26.154 100.124
   256  26.218    .000    .000    .000    .000  47.742  26.154 100.114
   257  26.209    .000    .000    .000    .000  47.742  26.154 100.105
   258  26.209    .000    .000    .000    .000  47.742  26.154 100.105

AVER:   26.222    .000    .000    .000    .000  47.742  26.154 100.118
SDEV:     .013    .000    .000    .000    .000    .000    .000    .013
SERR:     .005    .000    .000    .000    .000    .000    .000
%RSD:      .05   .0000   .0000   .0000   .0000     .00     .00

PUBL:   26.103    n.a.    n.a.    n.a.    n.a.  47.742  26.154  99.999
%VAR:      .46     .00     .00     .00     .00     .00     .00
DIFF:     .119     ---     ---     ---     ---    .000    .000
STDS:      522       0       0       0       0     ---     ---

I am attempting to measure these different emission lines at the same detector bias and only adjusting the gain to place the PHA peak a little to the right of center at a moderate beam current.  The idea being that as the count rate increases and the PHA experiences "pulse depression", the PHA peak will shift to the left, but still be within the range of the counting electronics.  All measurements are also done using "integral" mode.

I am looking at the data and looking for trends in the dead time constant as a function of emission energies, and I think I may be seeing something, but only between the 1 atm and 2 atm flow detectors.

It would be great to get some constant k-ratio measurements on a modern JEOL instrument with large area crystals with count rates exceeding 100K cps to compare...

[Probeman]

Now that our dead times are pretty well adjusted using the constant k-ratio method, we might be able to observe more subtle miscalibration issues such as the picoammeter calibration.

If ones picoammeter is miscalibrated, then the effect should be seen in all 5 spectrometers. Here are some plots where the intensities for all 5 spectrometers were aggregated using the aggregate feature in Probe for EPMA and the weight percent quantified. First for TiO2 using Ti metal as a primary standard (as a function of beam current):



and here for SrTiO3 again using Ti metal as a primary standard:



Although the effect is rather small we can see the offset between the 5 to 50 nA and the 50 to 500 nA range. We are attempting to obtain a high accuracy current source to calibrate our picoammeter and will let you know how it goes.